Cientistas descobrem uma fonte de energia escondida dentro de um buraco negro monstruoso

No coração da galáxia gigante M87 encontra-se o buraco negro M87*, que contém impressionantes seis mil milhões e meio de massas solares e gira rapidamente em torno do seu eixo. Usando a energia desta rotação, M87* alimenta um jato de partículas expelido quase à velocidade da luz, estendendo-se por imensos 5.000 anos-luz. Esses jatos também são gerados por outros buracos negros em rotação. Contribuem para dispersar energia e matéria por todo o universo e podem influenciar a evolução de galáxias inteiras.

Uma equipe de astrofísicos da Goethe University Frankfurt, liderada pelo Prof. Luciano Rezzolla, desenvolveu um código numérico, denominado código de partículas na célula de Frankfurt para espaços-tempos de buracos negros (FPIC), que descreve com alta precisão os processos que convertem energia rotacional em um jato de partículas. O resultado: além do mecanismo de Blandford-Znajek – que até agora tem sido considerado responsável pela extração de energia rotacional do buraco negro através de campos magnéticos fortes – os cientistas revelaram que outro processo está envolvido na extração de energia, nomeadamente, a reconexão magnética. Nesse processo, as linhas do campo magnético se quebram e se recompõem, fazendo com que a energia magnética seja convertida em calor, radiação e erupções de plasma.

O código FPIC simulou a evolução de um grande número de partículas carregadas e campos eletromagnéticos extremos sob a influência da forte gravidade do buraco negro. Claudio Meringolo, principal desenvolvedor do código, explica: “Simular tais processos é crucial para a compreensão da dinâmica complexa de plasmas relativísticos em espaços-tempos curvos próximos a objetos compactos, que são governados pela interação de campos gravitacionais e magnéticos extremos”.

As investigações exigiram simulações de supercomputadores altamente exigentes que consumiram milhões de horas de CPU no supercomputador “Goethe” de Frankfurt e no “Hawk” de Stuttgart. Este grande poder computacional foi essencial para resolver as equações de Maxwell e as equações de movimento de elétrons e pósitrons de acordo com a teoria da relatividade geral de Albert Einstein.

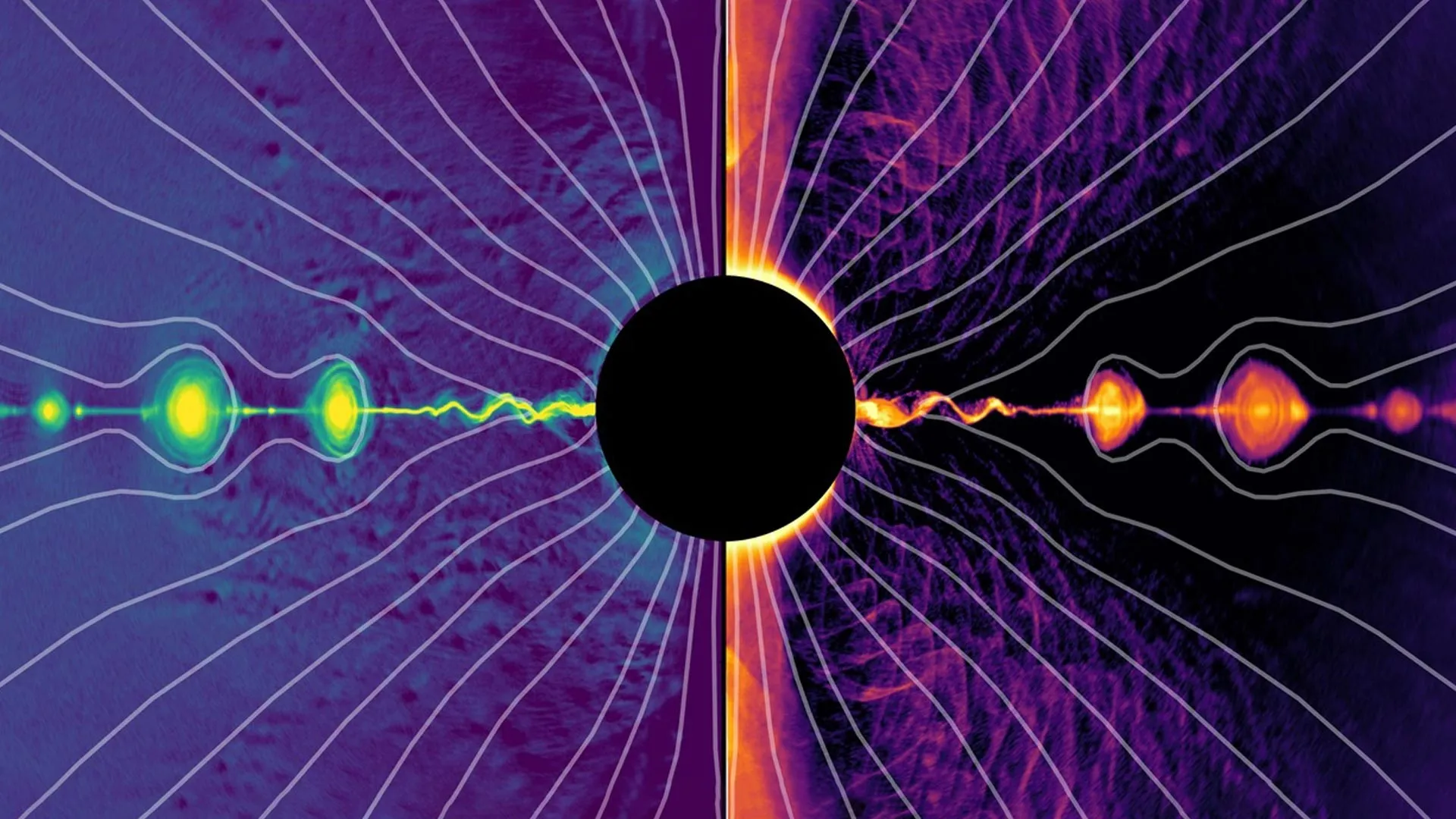
No plano equatorial do buraco negro, os cálculos dos investigadores revelaram intensa atividade de reconexão, levando à formação de uma cadeia de plasmóides – uma condensação de plasma em “bolhas” energéticas – movendo-se quase à velocidade da luz. Segundo os cientistas, esse processo é acompanhado pela geração de partículas com energia negativa que são utilizadas para alimentar fenômenos astrofísicos extremos, como jatos e erupções de plasma.

“Os nossos resultados abrem a fascinante possibilidade de que o mecanismo Blandford-Znajek não seja o único processo astrofísico capaz de extrair energia rotacional de um buraco negro,” diz o Dr. Filippo Camilloni, que também trabalhou no projecto FPIC, “mas que a reconexão magnética também contribui”.

“Com o nosso trabalho, podemos demonstrar como a energia é extraída de forma eficiente de buracos negros em rotação e canalizada em jatos”, diz Rezzolla. “Isso nos permite ajudar a explicar as luminosidades extremas dos núcleos galácticos ativos, bem como a aceleração das partículas quase à velocidade da luz.” Ele acrescenta que é incrivelmente emocionante e fascinante compreender melhor o que acontece perto de um buraco negro usando códigos numéricos sofisticados. “Ao mesmo tempo, é ainda mais gratificante poder explicar os resultados destas simulações complexas com um tratamento matemático rigoroso – como fizemos no nosso trabalho.”